Finite State Automata

Finite state automata adalah mesin abstrak berupa sistem model matematika dengan masukan dan keluaran diskrit yang dapat mengenali bahasa paling sederhana (bahasa reguler) dan dapat diimplementasikan secara nyata.

Finite State Automata (FSA) adalah model matematika yang dapat menerima input dan mengeluarkan output yang memiliki state yang berhingga banyaknya dan dapat berpindah dari satu state ke state lainnya berdasarkan input dan fungsi transisi. Finite state automata tidak memiliki tempat penyimpanan/memory, hanya bisa mengingat state terkini.

Finite State Automata didefinisikan sebagai pasangan 5 tupel → M =(Q, ∑, δ, S, F).

Q : himpunan hingga state
∑ (Sigma) : himpunan hingga simbol input (alfabet)
δ (Delta) : fungsi transisi, menggambarkan transisi state FSA akibat pembacaan simbol input. Fungsi transisi ini biasanya diberikan dalam bentuk tabel.
S ∈ Q : state AWAL
F ⊆ Q : himpunan state AKHIR

Contoh 1:

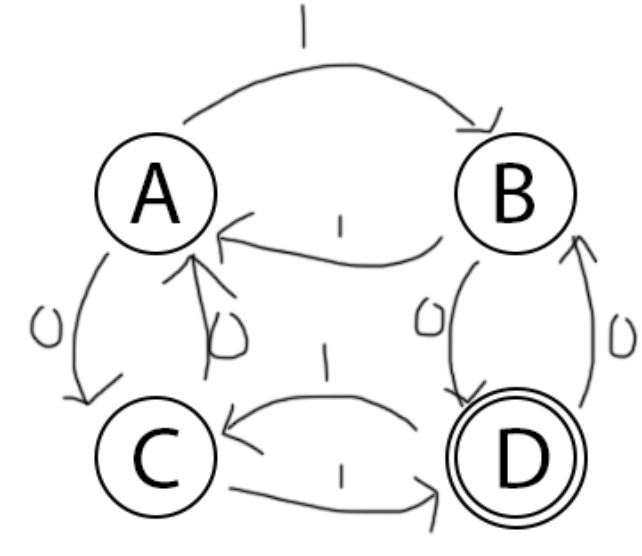
Keterangan:

• A, B, C, dan D merupakan state yang dinaungi oleh lingkaran
• A merupakan state awal
• Lingkaran ganda merupakan state akhir / final state
• Busur menyatakan transisi. Contoh jika A diberi input 1 maka transisi nya yaitu A ke B.

Q = {A, B, C, D}

∑ = {0,1}

S = A

F = D

δ (Delta) :

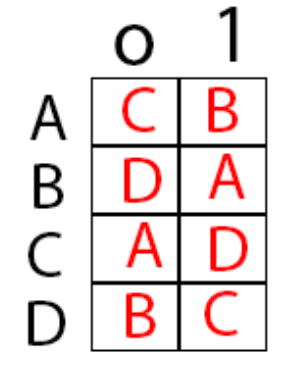
Untuk membaca tabel transisi diatas, state A jika diinput 0 maka akan menuju state C. Dan jika diinput 1 maka akan menuju state B. Dan seterusnya.

Contoh 2:

Seorang petani dengan seekor serigala, kambing dan seikat rumput berada pada suatu sisi sungai. Tersedia hanya sebuah perahu kecil yang hanya dapat dimuati dengan petani tersebut dengan salah satu serigala, kambing atau rumput. Petani tersebut harus menyeberangkan ketiga bawaannya kesisi lain sungai. Tetapi jika petani meninggalkan serigala dan kambing pada suatu saat, maka kambing akan dimakan serigala. Begitu pula jika kambing ditinggalkan dengan rumput, maka rumput akan dimakan oleh kambing. Mungkinkah ditemukan suatu cara untuk melintasi sungai tanpa menyebabkan kambing atau rumput dimakan.

Dari soal diatas, bisa diambil beberapa kombinasi state menjadi seperti berikut:

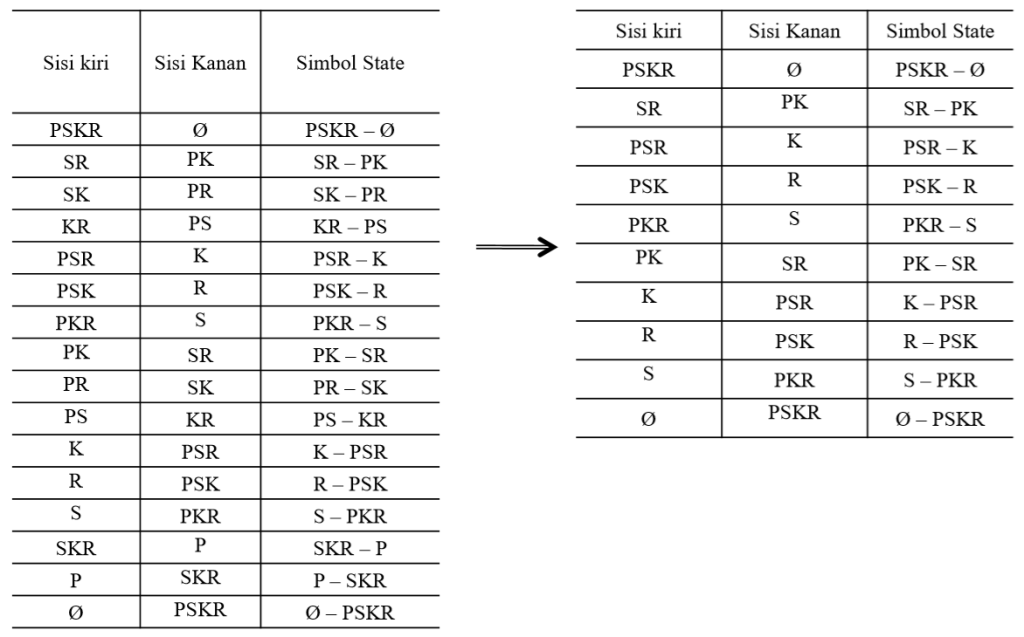
Dan dari 16 kombinasi state tersebut, hanya 10 state yang memenuhi syarat.

Lalu dari state diatas dibuatlah diagram transisi.

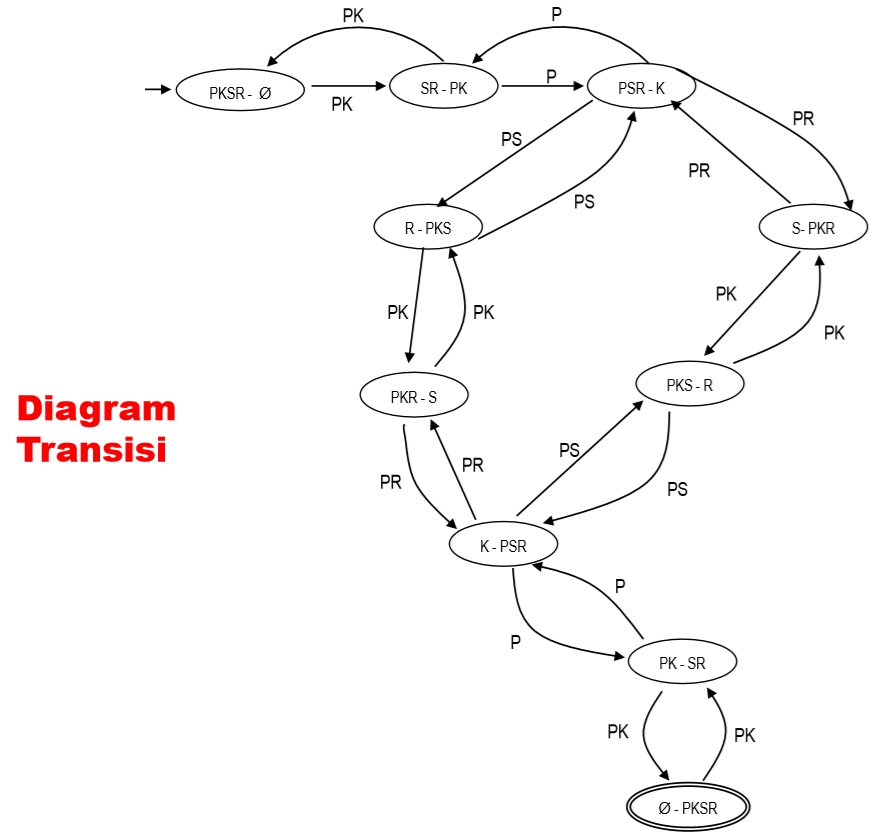
Lalu tupel dari state diatas adalah:

M = (Q, ∑, δ, S, F)

Q = {PKSR-Φ, SR-PK, PSR-K, R-PSK, S-PKR, PKR-S, PSK-R, K-PSR, PK-SR, Φ-PKSR}

Σ = {p, k, s, r}

S = PKSR –Φ

F = {Φ-PKSR}

Deterministic Finite Automata

Deterministic Finite Automata adalah model komputasi tersimpel dalam Finite automata. Khas dari DFA adalah DFA mempunyai memori yang sangat terbatas.

Deterministic finite automata (DFA) → M = (Q, ∑, δ, S, F), dimana :

Q : himpunan state/kedudukan

∑ : himpunan simbol input

∂ : fungsi transisi, dimana ∂ ∈ Q x ∑ → Q

S : State awal (initial state)

F : himpunan state akhir (Final State)

Language → L(M) : (x| ∂(S,x) di dalam F)

Contoh 1:

L1 = kumpulan String yang dimulai dari ‘0’

= {0, 00, 01, 001, 010, 011, 000, 0000, 011001, … }

Dari string tersebut, selanjutnya membuat desain dari DFA.

Untuk membuat desain, langkah pertama adalah membuat initial state atau state awal. Disini saya menggunakan Label A untuk state awal.

Langkah 1 :

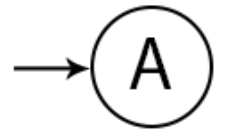
Langkah 2, selanjutnya karena saya akan menginput ‘0’ maka akan dikirimkan ke state berikutnya yaitu state B:

Langkah 3, pada sudah di state B, di state B bisa saja mendapatkan input 0 atau 1, maka:

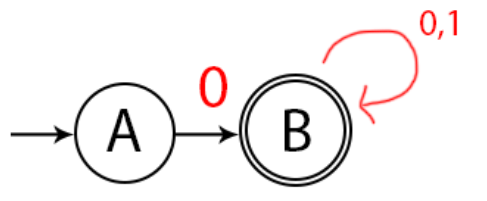
Langkah 4, lalu bagaimana jika pada state A akan diinputkan 1? Jika state A diinputkan angka 1, maka dibuatlah state C.

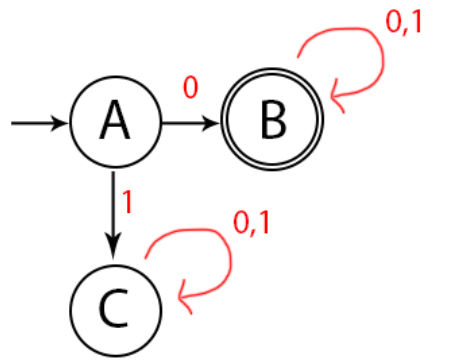
Karena state C tidak bisa pergi ke final state, maka state C disebut Dead State atau Trap State karena setelah berada di state C, tidak akan bisa pergi kamanpun.

Pengecekan / Penelusuran

Contoh 1, cek apakah 001 accepted?

Karena string berakhir di state B, dimana state B adalah final state, maka string tersebut diterima / accepted.

Contoh 2, cek apakah 101 diterima?

Karena string berakhir di state C yang mana state C adalah Dead State dan tidak berakhir di final state, maka string tersebut tidak diterima.

Contoh 2:

Bangunlah DFA yang menerima semua string dengan {0,1} dengan panjang stringnya adalah 2.

∑ = {0,1}

L = {00,01,10,11}

Selanjutnya buatlah desain DFA dari soal diatas.

Langkah 1, buatlah state awal, diikuti dengan inputan 0 atau 1.

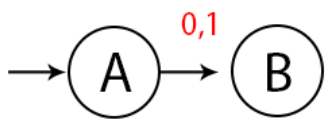
Langkah 2, kita sudah mendapatkan string dengan panjang 1. Lalu buatlah state lagi supaya mendapatkan panjang 2.

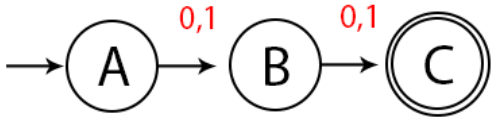
Langkah 4:

Kita sudah mendapatkan panjang string 2. Lalu karena pada state C kita belum menambahkan input apa-apa, maka jika pada state C mendapatkan inputan 0 atau 1 maka dibuatlah state D dan lakukan looping jika ada inputan pada state D.

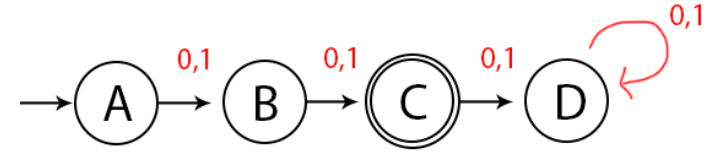
Pengecekan / Penelusuran

Contoh , cek apakah 00 diterima?

Karena string terakhir berada pada final state, maka string 00 diterima.

Non-Deterministic Finite Automata

Sebelum melanjutkan materi, mari kita review kembali materi DFA supaya mendapat gambar untuk NFA (non-deterministic finite automata).

DFA

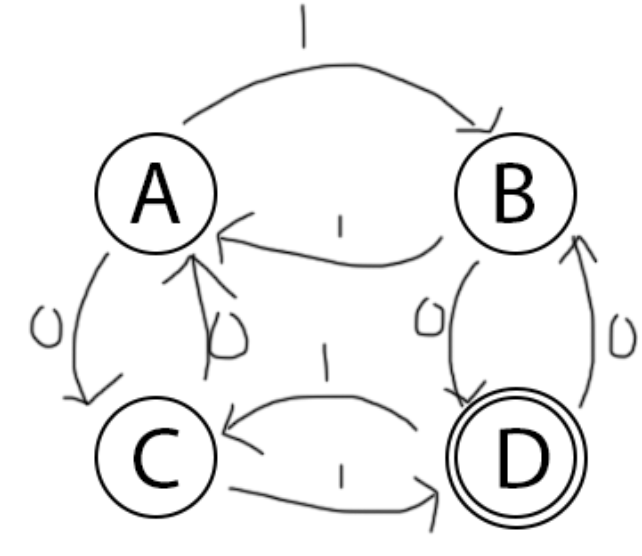
• Di DFA, kita tahu state apa selanjutnya jika ada inputan.
• DFA mempunya satu state unik, artinya hanya masing-masing state tidak ada yang sama.
• Kita tidak bisa memilih state selanjutnya.
• Simpel dan mudah untuk di desain.

NFA

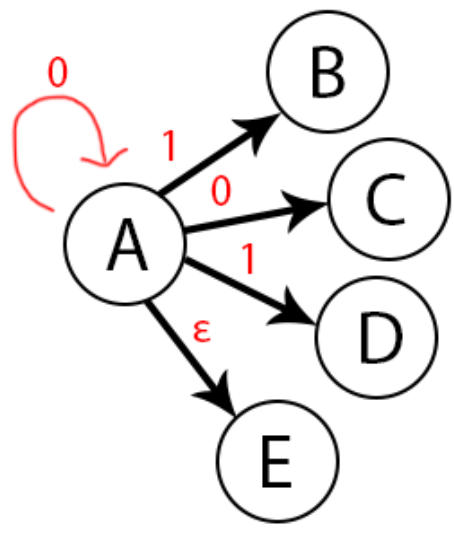
• Di NFA, saat diberi inputan, ada kemungkinan dapat beberapa state / multiple state. Bisa kita lihat pada gambar diagram diatas, saat diberi inputan 0 pada state A, state yang mungkin dipilih adalah state A sendiri atau state D.
• State selanjutnya mungkin terpilih secara random.
• Semua state selanjutnya mungkin terpilih secara pararel.

Contoh 1 dari NFA

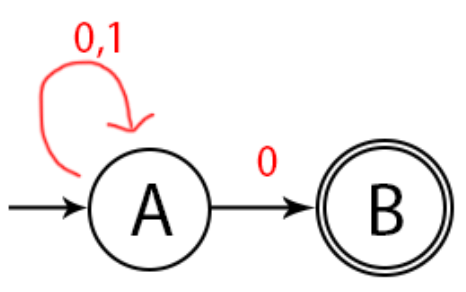
L = {kumpulan string yang diakhiri oleh 0}

Dari NFA diatas, bisa dilihat bahwa pada state A, jika diberi inputan 0, ada dua kemungkinan yaitu ke state A sendiri atau ke state B. Hal ini disebut multiple state. Lalu apa yang terjadi jika B tidak diberi inputan? pada NFA, hal ini dibolehkan. Jika state B tidak diberi inputan, itu menyatakan bahwa state B tidak pergi ke state apapun.

NFA → M = (Q, ∑, δ, S, F) dimana:

Q : himpunan state/kedudukan

∑ : himpunan simbol input

S : State awal (initial state)

F : himpunan state akhir (Final State)

∂ : Q x ∑ → 2^Q

Pengecekan / Penelusuran

Contoh , cek apakah 100 diterima?

Pertama, buat dahulu state awal. Lalu jika diberi inputan 1, maka akan pergi ke state A sendiri (loop)

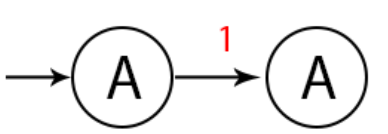
Lalu selanjutnya akan diberi inputan 0. Disini ada dua state, yaitu ke state A dan ke state B.

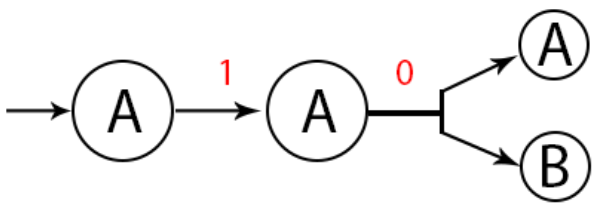
Pertama kita coba dahulu di state A. Input string selanjutnya yaitu 0, maka ada dua state juga yaitu state A dan B. Jika kita pergi ke state B maka string tersebut diterima karena sudah final state.

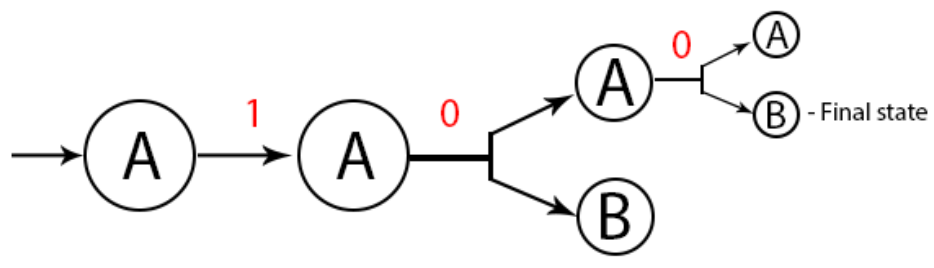
Gambar diatas mungkin terlihat sudah selesai, tapi kita belum mengecek pada state B. Jika kita lihat bahwa state B menyatakan tidak mempunyai inputan yang berarti tidak pergi kemanapun.

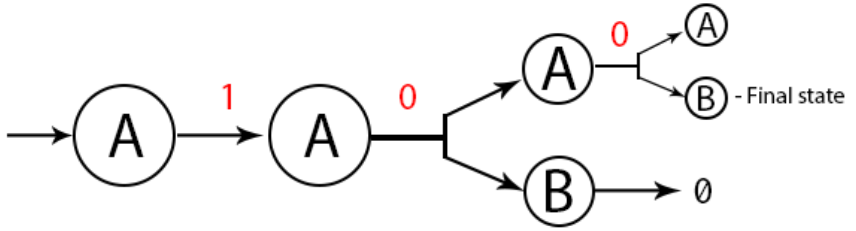
Bisa kita lihat bahwa pada sebelum state B adalah final state, namun state A kosong. Hal ini diperbolehkan karena paling sedikit satu state adalah final state dan jika sudah terpenuhi maka string tersebut dapat diterima.

Conversion of NFA to DFA

Setiap DFA adalah NFA, tapi tidak sebaliknya. Tetapi adalah juga DFA yang ekuivalen / setara dengan NFA.

Contoh :

L = {kumpulan semua string (0,1) yang diawali dengan 0}

∑ = {0,1}

Pertama, kita gambarkan dulu gambar dari NFA.

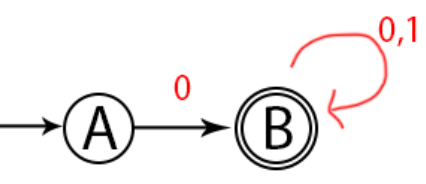
Lalu kita buatkan digram transisinya.

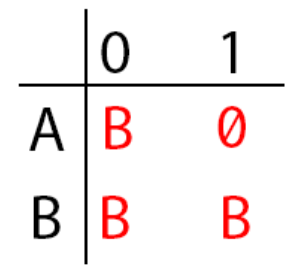
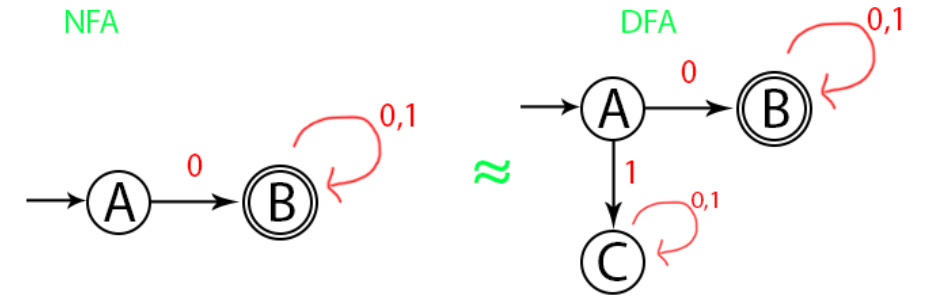
Selanjutnya kita buatkan digram DFA untuk membuat perbandingan.

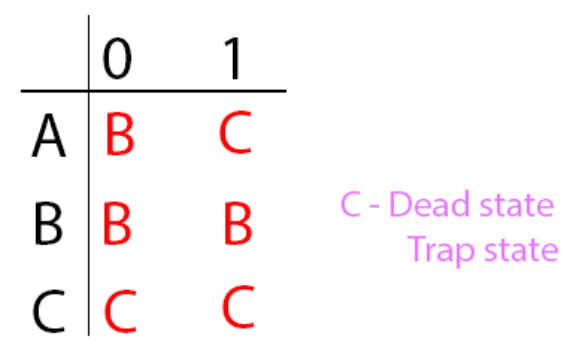
Lalu kita gambarkan gambar dari DFA.

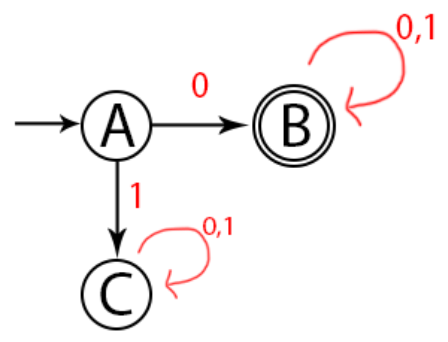
Dari perbandingan diatas, NFA dan DFA adalah ekuivalen setelah dikonversi.

Ekuivalensi Antar Deterministic Finite Automata

Dua DFA M1 dan M2 dinyatakan ekivalen apabila L(M1) = L(M2)

Reduksi Jumlah State

Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efisiensi).

State pada FSA dapat direduksi apabila terdapat useless state.

Hasil dari FSA yang direduksi merupakan ekivalensi dari FSA semula.

Pasangan Statedapat dikelompokkan berdasarkan:

• Distinguishable State (dapat dibedakan) Dua state p dan q dari suatu DFA dikatakan indistinguishable apabila: δ(q,w) ∈ F dan δ(p,w) ∈ F atau δ(q,w) ∉ F dan δ(p,w) ∉ F untuk semua w ∈ S*
• Indistinguishable State ( tidak dapat dibedakan) Dua state p dan q dari suatu DFA dikatakan distinguishable jika ada string w ∈S* hingga: δ(q,w) ∈F dan δ(p,w) ∉

Relasi

Pasangan dua buah state memiliki salah satu kemungkinan : Distinguishable atau indistinguishable tetapi tidak kedua-duanya.

Dalam hal ini terdapat sebuah relasi:

Jika p dan q indistinguishable,

dan q dan r indistinguishable,

maka p, r indistinguishable dan

p,q,r indistinguishable.

Dalam melakukan eveluasi state, didefinisikan suatu relasi : Untuk Q yg merupakan himpunan semua state

• D adalah himpunan state-state distinguishable, dimana D ⊂ Q
• N adalah himpunan state-state indistinguishable, dimana N ⊂ Q
• maka x ∈ N jika x ∈ Q dan x ∉ D

Step – Step dalam melakukan Reduksi

• Hapuslah semua state yg tidak dapat dicapai dari state awal (useless state)
• Buatlah semua pasangan state (p, q) yang distinguishable, dimana p ∈ F dan q ∉F. Catat semua pasangan-pasangan state tersebut.
• Cari state lain yang distinguishable dengan aturan: “Untuk semua (p, q) dan semua a ∈ ∑, hitunglah δ (p, a) = pa dan δ (q, a) = qa” Jika pasangan (pa, qa) adalah pasangan state yang distinguishable maka pasangan (p, q) juga termasuk pasangan yang distinguishable.
• Semua pasangan state yang tidak termasuk sebagai state yang distinguishable merupakan state-state indistinguishable.
• Beberapa state yang indistinguishable dapat digabungkan menjadi satu state.
• Sesuaikan transisi dari state-state gabungan tersebut.

Contoh :

Sebuah Mesin DFA:

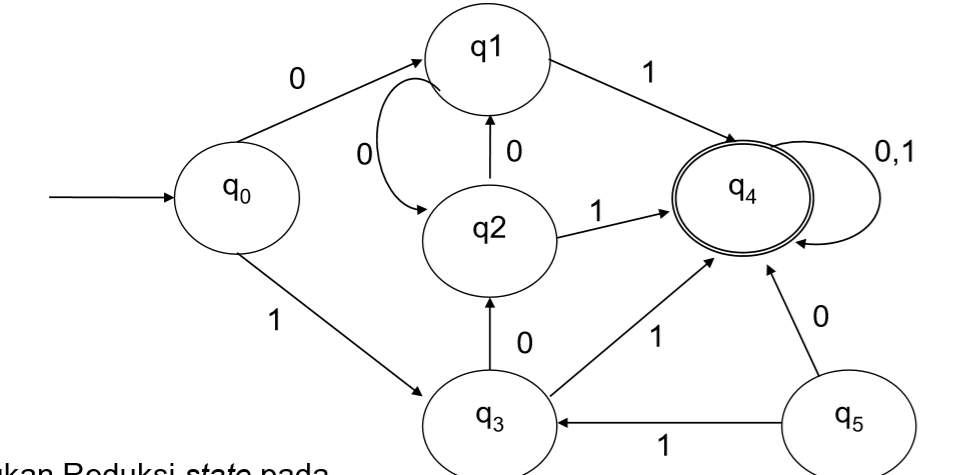
Lakukan Reduksi state pada DFA diatas?

• State q5 tidak dapat dicapai dari state awal dengan jalan apapun (useless state). Hapus state q5
• Catat state-state distinguishable, yaitu : q4 ∈ F sedangkan q0, q1, q2, q3 ∉ F sehingga pasangan (q0, q4) (q1, q4) (q2, q4) dan (q3, q4) adalah distinguishable.
• Pasangan-pasangan state lain yang distinguishable diturunkan berdasarkan pasangan dari langkah 2, yaitu :
• Untuk pasangan (q0, q1) : δ(q0, 0) = q1 dan δ(q1, 0) = q2 → belum teridentifikasi δ(q0, 1) = q3 dan δ(q1, 1) = q4 → (q3, q4) distinguishable maka (q0, q1) adalah distinguishable.
• Untuk pasangan (q0, q2) : δ(q0, 0) = q1 dan δ(q2, 0) = q1 → belum teridentifikasi δ(q0, 1) = q3 dan δ(q2, 1) = q4 → (q3, q4) distinguishable maka (q0, q2) adalah distinguishable.
• Setelah diperiksa semua pasangan state maka terdapat state-state yang distinguishable : (q0,q1), (q0,q2), (q0,q3), (q0,q4), (q1,q4), (q2,q4), (q3,q4) Karena berdasarkan relasi-relasi yang ada, tidak dapat dibuktikan (q1, q2), (q1, q3) dan (q2, q3) distinguishable, sehingga disimpulkan pasangan pasangan state tersebut indistinguishable.
• Karena q1 indistinguishable dengan q2, q2 indistinguishable dengan q3, maka dapat disimpulkan q1, q2, q3 saling indistinguishable dan dapat dijadikan satu state.
• Berdasarkan hasil diatas makahasil dari DFA yang direduksi menjadi:

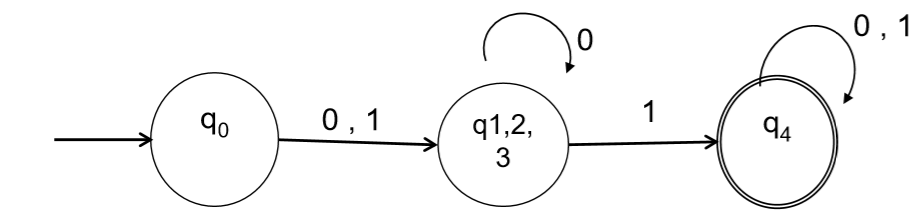
Daftar Pustaka

Priska Simaremare. 2013. Finite State Automata. di https://riskasimaremare.wordpress.com/2013/04/23/finite-state-automata/ (diakses tanggal 25 April 2020)

Neso Academy. (Dec 24, 2016). Finite State Machine (Finite Automata). [berkas video]. Diakses di https://www.youtube.com/watch?v=Qa6csfkK7_I&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=3

Neso Academy. (Dec 18, 2016). Deterministic Finite Automata (Example 1). [berkas video]. Diakses di https://www.youtube.com/watch?v=40i4PKpM0cI&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=4

Neso Academy. (Dec 19, 2016). Deterministic Finite Automata (Example 2). [berkas video]. Diakses di https://www.youtube.com/watch?v=2KindKcLjos&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=5

Neso Academy. (Dec 24, 2016). Non-Deterministic Finite Automata. [berkas video]. Diakses di https://www.youtube.com/watch?v=ehy0jGIYRtE&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=10

Neso Academy. (Dec 24, 2016). Formal Definition of Non-Deterministic Finite Automata (NFA). [berkas video]. Diakses di https://www.youtube.com/watch?v=egXhe55dAIk&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=11

Neso Academy. (Dec 26, 2016). FNon-Deterministic Finite Automata (Solved Example 1). [berkas video]. Diakses di https://www.youtube.com/watch?v=4bjqVsoy6bA&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=12